“The death of one man is a tragedy.
The death of millions is a statistic.”
Josef Stalin, comment to Churchill at Potsdam, 1945
I had an interesting discussion the other day about methods that focus on group differences and what they mean for individual fairness. Thinking about it (and tidying up my thoughts), it goes like this:
Roughly speaking, in many scientific disciplines, scientists use statistical methods to determine whether differences in the data, e.g., of treatments, or between groups, are “real”. After all, you draw a sample and you could be unlucky. Such a statistical method tells you how likely it is that you get this data given the assumption that there are no differences between the groups. If that likelihood is sufficient small (usually less than .05 or 5%), scientists assume that there “really is a difference”. A smart and highly useful method to look for differences. (That was very, very superficial explanation and this method got a bulk of problems, but that’s something for another posting.)
Here I want to focus on the consequences when you make conclusions based on statistically significant differences between two groups. I think that this group-based view can obscure a lot of detail.
Let’s look at the following two groups:
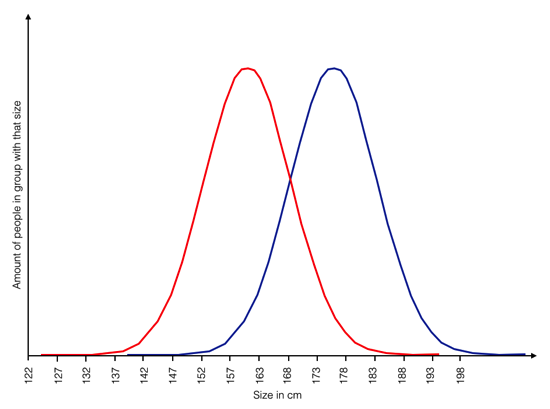
What you can see is that the blue group is on average larger than than the red group. And there is quite a gap. The average person in the blue group is roughly 15 cm taller than the average person in the red group. The data are taken from a size chart by OK Cupid, showing the distribution of US women (red) and US men (blue). (There might be small deviations, drawing with the mouse isn’t that easy and the copy and paste was messy.)
So the gap is there, and while I haven’t calculated a test of statistical significance, let’s assume it actually is statistically significant. You could say, poor red group. Just imagine there’s a shelf that requires you to be at least 173 cm tall to reach the top of it.
As you can see in the following graphic, the red group really is disadvantaged here. Given that they are smaller on average many more people in the red group are affected than in the blue group. The average person in the blue group can reach the top of the shelf, the average person in the red group cannot:
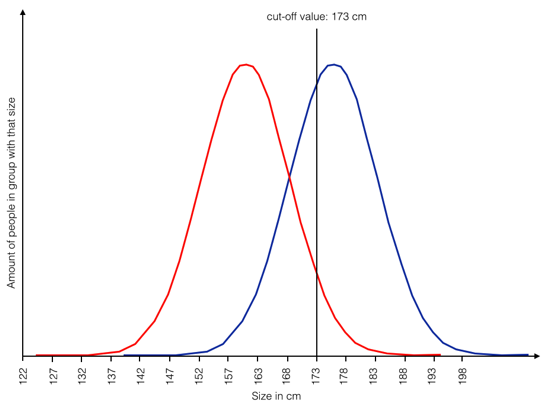
Now imagine the usual reasoning following these measurements: We must do something for the red group. They are smaller, they are affected more (at least in quantity/percentages), we have to help them.
The problem with this kind of reasoning becomes clear in the next two graphics:
Yes, more people in the red group are affected, but that does not mean that every person in the red group is affected. The ones in the red-filled area are not:
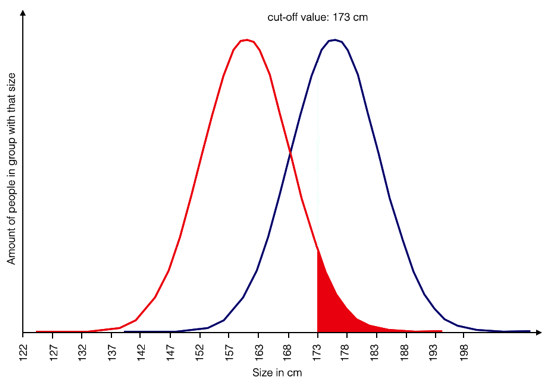
Making it an issue of being a member of the red group implies that every person in it is too small. But the ones larger than 173 cm are not affected. They don’t need the support and they probably would not like being called affected. In short, it makes the red group look deficient — and quite wrongly.
There’s also the — usually neglected — flip side. The ones in the blue group who are smaller than 173 cm. Sure, there aren’t that many, less than 50% (blue-filled in the following graphic):
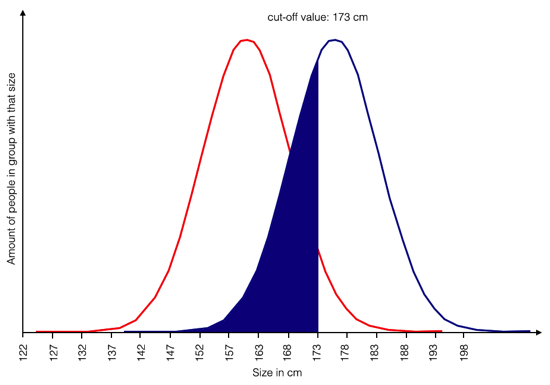
They are being ignored if the support focuses only on the members of the red group. And yup, while they would still beat most members of the red group in height, they cannot reach that top shelf either. But given that most of their group can they are seen as irrelevant.
And all this while the overall conclusions:
- the red group is significantly smaller than the blue group, and
- the red group is much stronger affected by a shelf requires you to be at least 173 cm tall
remain perfectly true.
The questions that are not asked here are:
- How many people do you wrongly assume to be affected (the red ones taller than 173 cm, aka “false alarms”)? and
- How many people do you wrongly assume to be unaffected (the blue ones smaller than 173 cm, aka “miss”)?
This is a problem in reasoning based on group membership, even if the groups differ significantly. Is pretty easy to see when it comes to height. No one would build a step stool only for women (I hope). But it is more difficult to see when it comes to other variables. For example, imagine something like social confidence instead of height on the x-axis. Also known as “voices ideas in meetings”. The distributions are likely similar.
Just because on average one group is more affected than the other, in reality or in public perception, does not mean that you can neglect all members of the “unaffected” (= less affected) group. The question again is: How many do you falsely accuse of having a problem, and how many people with problems do you miss.
I don’t know, it was an interesting discussion, and on the bright side, I think it lead to a nice illustration of a common problem. The focus on one very salient and very popular variable (here: sex/gender) obscures what actually matters: the individuals.
Update:
The example of height is interesting in another aspect I did not consider before. Suppose the overall goal would be equal representation with both groups. Ignore individuals, let’s assume kin liability (worked for Nazi Germany and still works for North Korea). If enough others of “your group” (which you did not chose) can reach the top of the shelf, who cares that you cannot do it. Not something I would support, but let’s assume this were the goal.
Then you have a couple of possibilities:
a) cull those in the blue group between 173 and roughly 188 cm
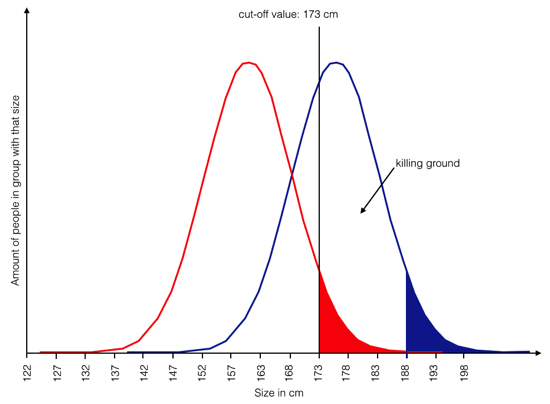
The ones in the blue group above 188 cm are about as many as those in the red group above 173 cm. Discourage those in the blue group between 173 cm and 188 cm from ever trying or put a bullet in each kneecap. No matter how you do it, you have to remove them. It’s #killallmen173to188cm. This way, a similar number in each groups will reach the top shelf. No, no one would do it (I hope), but if you go for groups and ignore individuals, that would be one conclusions. Albeit one that puts you in one “group” with genocidal maniacs.
b) weaken the blue population to be identical with the red one
In case of height, less food might work, or perhaps some genetic engineering. With other variables, discouragement, shame, etc. might work wonders. Perhaps some indoctrination. The overall effect: Much fewer people will be able to reach the top shelf. And you have crippled a group in the process, for no other crime than being a member of a group they did not chose (and you did not like the result when you plotted the data).
c) increase the whole red population to be identical with the blue one
As with others, intensive training and perhaps stimulants, perhaps some genetic engineering, might work here. That’s probably the naive understanding of support for only one group, no matter that there still would be about 40% who cannot make the cut (the ones in the blue group — now also the red group — smaller than 173 cm). People who do not get support to reach the top shelf.
It raises the question whether all members in the red group would be willing to pay the price — you are essentially doing social engineering.
And you might still miss a lot of people, in each group, who are smaller than 173 and want to get to that top shelf. Why is an overall change on group basis more important than the decision of individuals whether they want to reach the top shelf or not, no matter the group they are in?
d) a mixture of b) and c)
To meet somewhere in the middle between the two groups, meaning less people making the cut in the blue group, and likely, overall. You push the red group, punish the blue one, for less overall performance. Basically, you get the disadvantages of b) and c) too.
e) provide support for members of the red group, but only those larger than 157 cm and smaller than 173 cm
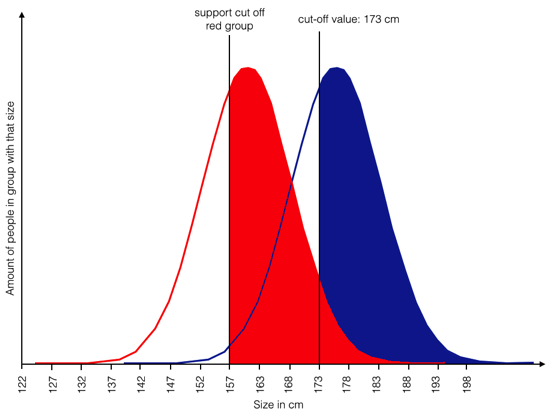
This would lead to similar amounts of people in both groups reaching the top shelf (and more overall), the ones in the red group between 157 cm and 173 cm, and the ones in the blue group without any support. Of course, few if any programs discriminate after a group variable is used. Programs usually are for all members of a group, diagnostics seem strangely absent. Makes sense, if performance is measured, they question becomes: Why not go for performance in the first place?
Furthermore, how would both groups work together, when people in the blue group can do it without support, while only a few in the red group can? The contact hypothesis states that people working together (to remove prejudices) have to be similarly competent others. This wouldn’t be the case here. Don’t get me wrong, there’s nothing wrong with getting training to reach a certain standard of performance. On the contrary. You need to train to become good in anything. But this training was offered only to one group, based on a variable they did not chose. The blue ones, esp. those below 173 cm, never had the same opportunity. That screams unfairness and preferential treatment.
And how do members of the blue group who cannot reach the shelf feel, when members of the red group, who are smaller than they are, are supported, while they are not. That leads to a lot of resentment, esp. when the overall message is: The group doesn’t count, people are equal. Reality paints a different picture. But then again, if you make your business by profiting from dissent between groups, that’s a plus. No matter how the ones affected feel.
Temporary Conclusion
It’s really interesting to see what happens when you take such a variable as height and use a cut-off value, an external criteria of performance that has to be kept. And like written, in a) to e), personal freedom goes right out the window, individuals are reduced not only to their group membership (which they did not chose) but also judged by how their group performs.
This kin-liability might be suitable when it comes to freely chosen group. If your group harasses people and is obnoxious, you can be damn sure I judge you by your affiliation. But this isn’t freely chosen, nor that relevant. Unless you solely focus on the group membership and suddenly you see it everywhere and in everything. Perception is interpretation, and interpretation can be biases and unfair.
After all, all individual members of each group have their own fates, their own dreams, their own aspirations. And for some, it’s to reach the top of the shelf, no matter how large they are, or how large others in “their group” are.